What we did
Step 1 – Building a database of cognates
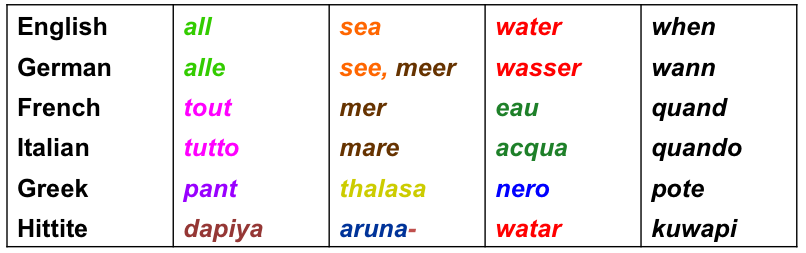
Cognates are similar words shared across languages and taken to indicate relatedness via common ancestry. To be diagnosed as cognate the words must have similar meaning and, most importantly, show systematic sound correspondences indicating a common origin. For example, the English word five has cognates in German (funf), Swedish (fem) and Dutch (vijf), reflecting descent from proto-Germanic (*fimf). Cognate identification can be tricky. For example, other cognates of these words for five include Irish cuig, Italian cinque, Armenian hing and Polish piec. Conversely, known borrowings, such as English mountain from French montagne, reflect more recent contact, rather than common ancestry, and so are not treated as cognate.
The table below shows an example dataset with six languages and cognate sets colour coded across four meanings.
We compiled a database of word forms and cognacy judgements across 103 Indo-European languages (including 20 ancient languages) and 207 meanings. The meanings we used are basic vocabulary items – including kinship terms (mother, father), body parts (hand, ear, eye), terms for the natural world (water, fire) and basic verbs (to run, to walk, to push) – that are thought to be relatively universal and resistant to borrowing. The dataset was built up from existing sources using expert linguists to make the cognate judgements. We recorded the presence or absence of more than 6000 sets of cognate words across the languages in our sample. Our cognate data can be downloaded here.
Step 2 – Location data
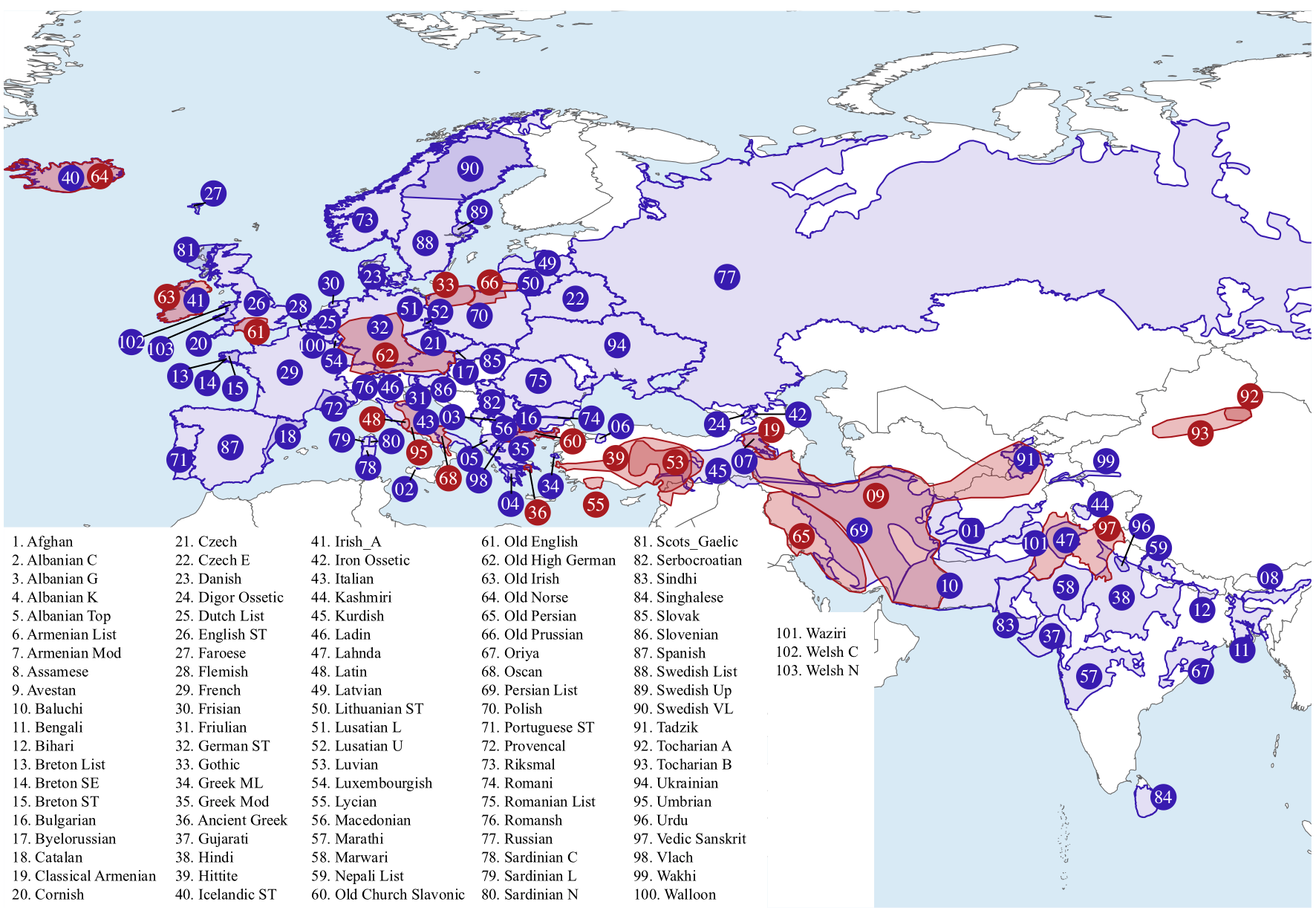
To work out where Indo-European languages have come from, we use information about where the contemporary languages in our sample are spoken today and where the ancient languages are thought to have been spoken. Rather than fixing each language to a single point location, we them an approximate range (Figure below).
Figure: Map showing language locations. Contemporary languages are shown in blue and ancient languages in red.
Step 3 – Building family trees of languages
Languages evolve through time in a manner similar to biological species. As groups of speakers become separated, their speech drifts apart forming new descendant languages, and eventually whole families of related languages. Over thousands of years this process has generated the 6000+ languages in the world today.
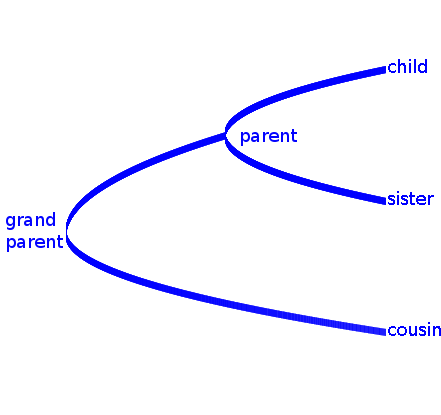
We can represent the relationships between languages on a family tree, otherwise known as a ‘phylogeny’. A simple example of a phylogeny is a family tree where the leaves of the tree represent the children in a family and branches represent relationships between parent and child.
Figure: small family tree with parent, child, grandparent (the common ancestor) and cousin
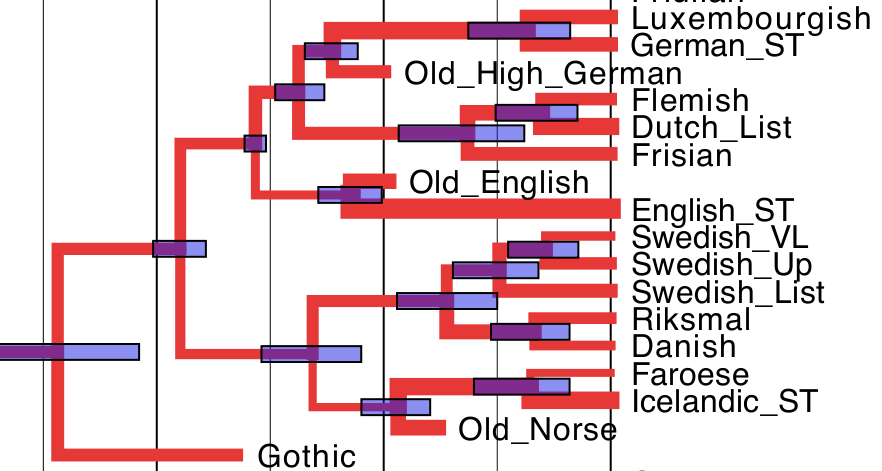
Likewise, a language phylogeny shows the family tree relationships between languages. Dutch and Flemish are sister languages that have a very recent common ancestor. English is a cousin language, which is a bit further away from Dutch and Flemish. The Scandinavian languages are distant cousins. The points where the branches of the tree come together represent older languages that gave rise to descendents in the tree.
Figure: Germanic languages
We model the evolution of Indo-European languages as the gain and loss of cognates along the branches of an unknown family tree, using an approach called Bayesian phylogenetic inference to infer the set of language trees that makes the cognate data most likely.
We explored a number of different models of cognate gain and loss, but the model that was best supported by the data was one that allows for variation in rates of evolution for different cognates (some words can evolve more quickly than others) and assumes that cognates are only ever gained once but can then be lost multiple times in descendent languages. This fits with linguists’ intuitions about the nature of cognate replacement – by definition, true cognates cannot be independently gained more than once and can then be lost multiple times at differing rates.
Step 4 – Calibrating the age of the tree
In order to provide a timescale for the expansion of the language family, we need some information about how fast languages change. We do this by constraining the age of known calibration points on the tree. For example, there is good reason to think that the Romance languages had begun to diverge by the time that the Roman Empire began to break up (often tied to the fall of Dacia in 270AD), so we can constrain the age of the sub-family based on that information. One advantage of the Bayesian approach is that we do not need to assume a specific age for any calibration, but can instead assign a range, the width of which depends on how confident we are in our prior beliefs about age of the group. Our analysis used 14 such known divergence times plus 20 extinct languages to calibrate rates of change across the tree.
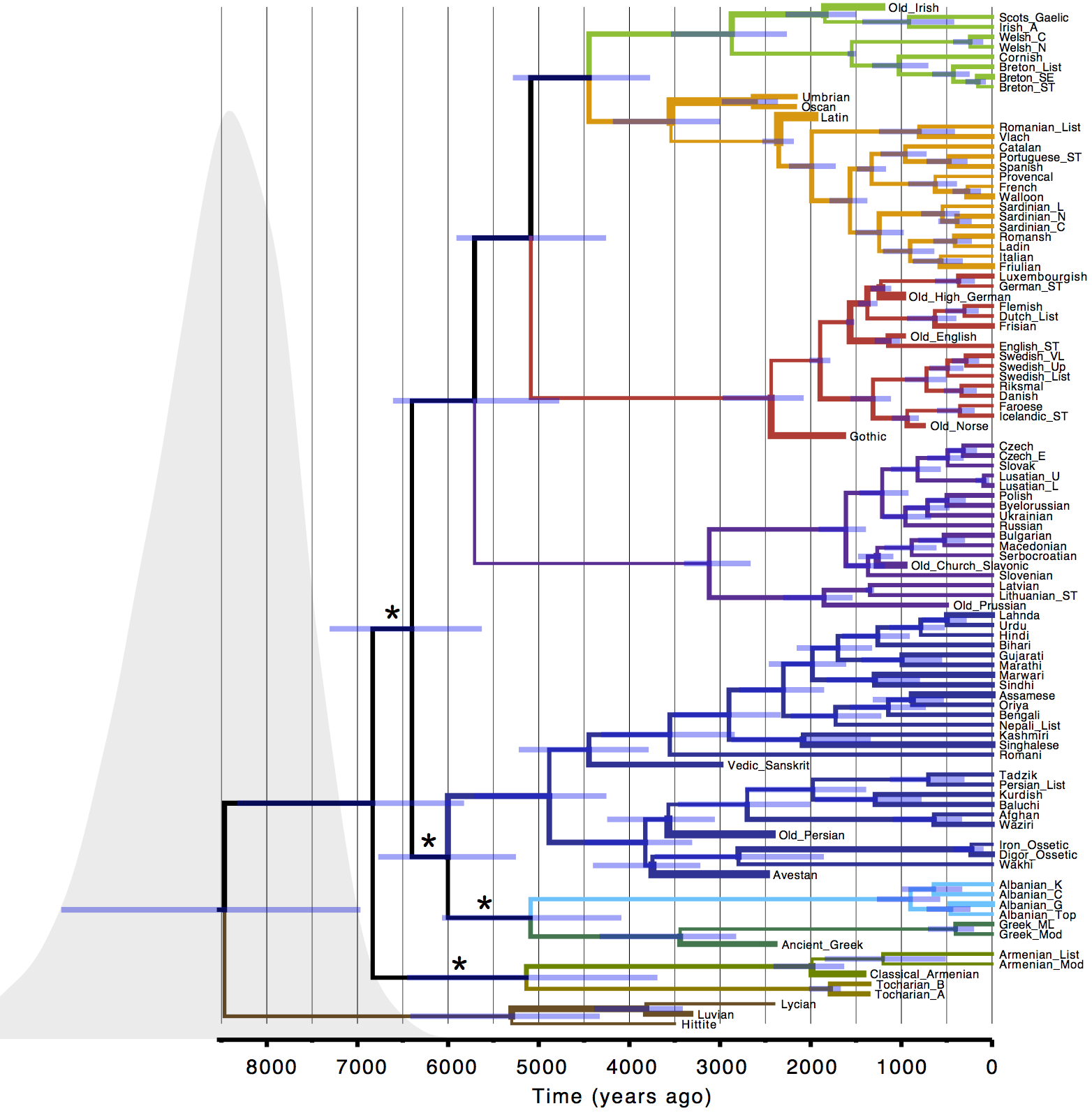
It is well known that rates of language change can vary through time, so rather than assuming a strict clock-like rate of cognate gain and loss, we allowed rates to vary along the branches of the tree. The amount of variation was itself estimated from the data. You can see the tree we inferred below, with a time scale along the bottom.
Figure: Inferred Indo-European language tree. The rate of evolution along each branch is represented by the thickness of the branch, where a thicker branch implies faster evolution.
Step 5 – Modelling language expansion
We combine our inferences about the Indo-European language family tree with information about where these languages are spoken (or were spoken in the case of the ancient languages). From the known locations at the ‘leaves’ of the tree, we can trace back along the branches to estimate the location at the root.
To do this, we adapt a Bayesian phylogeographic approach initially developed for tracing the origins of virus outbreaks, but rather than tracing viral lineages, we are tracing languages. The method models spatial diffusion of languages as a Brownian ‘random walk’ in two dimensions (latitude and longitude) along the branches of the tree. Put simply, this means that for a given time interval, the geographic distribution of languages expanding from some point of origin is assumed to be approximated by Brownian motion – some languages will have moved far, some will not have moved at all, but most will have moved somewhere in between. In fact, the assumptions of the model are even less restrictive because we ‘relax’ the random walk to allow the average rate of movement to vary across the tree – like with variation in rates of cognate replacement, the extent to which rates of expansion varied was estimated from our data.
Step 6 – Testing between the two homeland hypotheses
The Bayesian approach we employ means that we can directly test support for the Steppe homeland hypothesis versus the Anatolian homeland hypothesis. This is because the method we use does not produce a single answer – e.g. the homeland is at x degrees longitude and y degrees latitude. That would not be all that useful, because if you want to test between competing theories, you need some estimate of uncertainty – how sure are you that the origin is at one location versus another?
There is uncertainty in the relationships between the languages (nobody can say with absolute certainty that one particular family tree is the true one – for 103 languages there are more possible trees than there are atoms in the universe!), there is uncertainty in the time scale (we can’t know for sure exactly how fast languages change), and even if we knew the family tree and time scale exactly, there is uncertainty in the geographic expansion process so we cannot pin down the location of the root exactly.
One of the major advantages of the Bayesian approach is that we do not produce a single answer, but instead account for all those uncertainties using some clever algorithms (called Markov Chain Monte Carlos methods) that sample language trees, divergences times and locations at all points on the tree, in proportion to how likely they make our observed data. In terms of the origin location, if an origin is twice as likely, and we do not prefer any location over any other a priori, then we should see it twice as often in our sample.
So we were able to run our analyses and directly compare how often the origin locations we inferred fell in the range proposed for the Steppe theory versus in the range proposed for the Anatolian theory. In fact, we considered two different versions of the Steppe theory, just to make sure our findings were not contingent on the exact area ascribed to the theory.
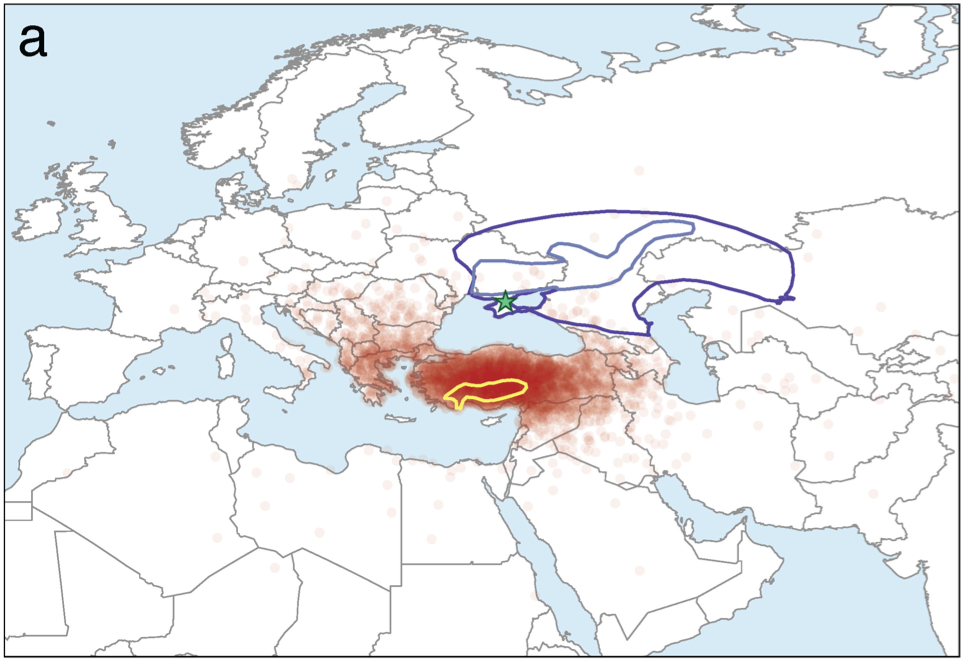
As we report in the paper, using either version of the Steppe theory, it was the Anatolian theory that came out on top. You can see this visually in our Figure 1, below. Virtually none of the points fall within the region implied by a Steppe origin. In the main table in our paper, we quantify this support using Bayes Factors, measuring the relative support for the Anatolian theory compared to either steppe theory. Our analysis finds that an Anatolian origin is orders of magnitude more likely than a Steppe origin.
Figure: Map showing the inferred geographic origin of the Indo-European language family. Our Markov chain Monte Carlo sampled locations are plotted in translucent red such that darker areas correspond to increased probability. The blue polygons delineate the proposed origin area under the Steppe hypothesis; dark blue represents the initial suggested Steppe homeland, and light blue denotes a later version of the Steppe hypothesis. The yellow polygon delineates the proposed origin under the Anatolian hypothesis. A green star in the steppe region shows the location of the centroid of the sampled languages.